前編の続きです。
前編ではコンピューターが2進数を扱うということを説明しました。
後編では2進数をうまく電気的な物理現象に関連付けて計算する方法を紹介していくのですが、まず結論から言ってしまうと電子回路というものを使うことで計算を実現します。
電子回路といっても難しいものではありません。とてもシンプルなものです。
小学校で電池と豆電球を使って実験した「直列つなぎ」とか「並列つなぎ」みたいなものです。👇
直列つなぎ

並列つなぎ
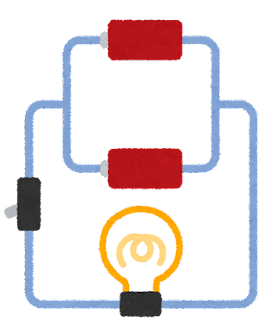
もうほとんど覚えていない人もいるかと思いますが、かつては誰しも「直列つなぎは豆電球が明るい!」とか「並列つなぎは電池が長持ち!」とか習ったはず。
「小学生でも分かる!」と謳っているのはこれが所以です。
小学生のころやった遊び感覚の実験が実はコンピューターが電気で計算する原理になっているのです!
これから3つの簡単な回路
- AND回路
- OR回路
- NOT回路
と、それらを組み合わせた一つの回路
- XOR回路
を紹介します。
そしてさらにその4つの回路を組み合わせることで電気を使った2進数の計算が可能になることを説明していきますので先人たちのアイディアの秀逸さを実感してもらえたら幸いです。
小学生の頃からの壮大な伏線回収ですね。
INDEX
直列つなぎでAND回路
直列つなぎは二つの電池の内どちらか一方でも切れてしまったら豆電球が点きません。
切れた電池の内部抵抗が大きくなって、電流が流れなくなってしまうからです。
両方とも電池の残量があって初めて豆電球を灯すことができます。
この性質を利用することでAND回路ができるのですが、電池の残量は見た目では分からないので、電池の代わりにスイッチに置き換えてみましょう。

左から右へと電気が流れ、間にスイッチを二つ挟んで豆電球へと続く図です。
この二つのスイッチを操作するために電磁石を使うことにしましょう。
電磁石は電気を流すことで磁力が発生します。

【A】に電流を流せば左のスイッチがONになり、【B】に電流を流せば右のスイッチがONになります。
どちらもONの時にしか豆電球は点灯しません。
豆電球をOUTとして、この関係をA、B、OUTについて表にまとめると以下のようになります。

1が電流が流れている。0が電流が流れていない。と考えてください。
・A、Bどちらも電流が流れていない(スイッチが繋がっていない)時は、もちろん豆電球も点かない。
・A、Bどちらかしか電流が流れていない(スイッチがどちらか一方だけしか繋がっていない)時も豆電球は点かない。
・A、Bどちらにも電流が流れている(スイッチがどちらも繋がっている)時にだけ、豆電球は点く。
という関係を表す表です。
(こういう入力の組み合わせと、それに対応した出力を並べた表を真理値表と言います)
実はこの関係が正しく論理積回路(AND回路)と呼ばれるものなのです。
AND回路の図は簡略化して👇このように書き、

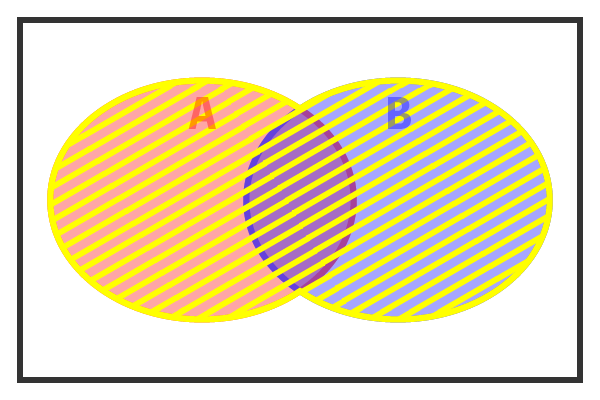
ベン図にしてみると斜線の部分を表します。
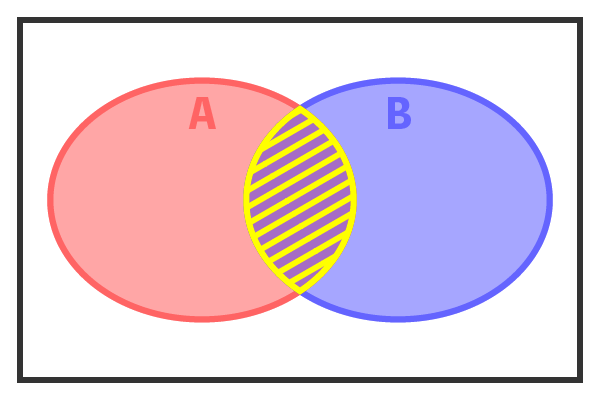
【A】と【B】がどちらも満たされている部分ですね。
並列つなぎはOR回路
直列とは違い、並列つなぎでは一つの電池が切れていても、もう一方の電池が生きていれば電流が流れるので豆電球が点きます。
二つとも電池が切れている場合のみ豆電球が点かないということです。
直列の時と同じように電池をスイッチに置き換えた図はこちらです。
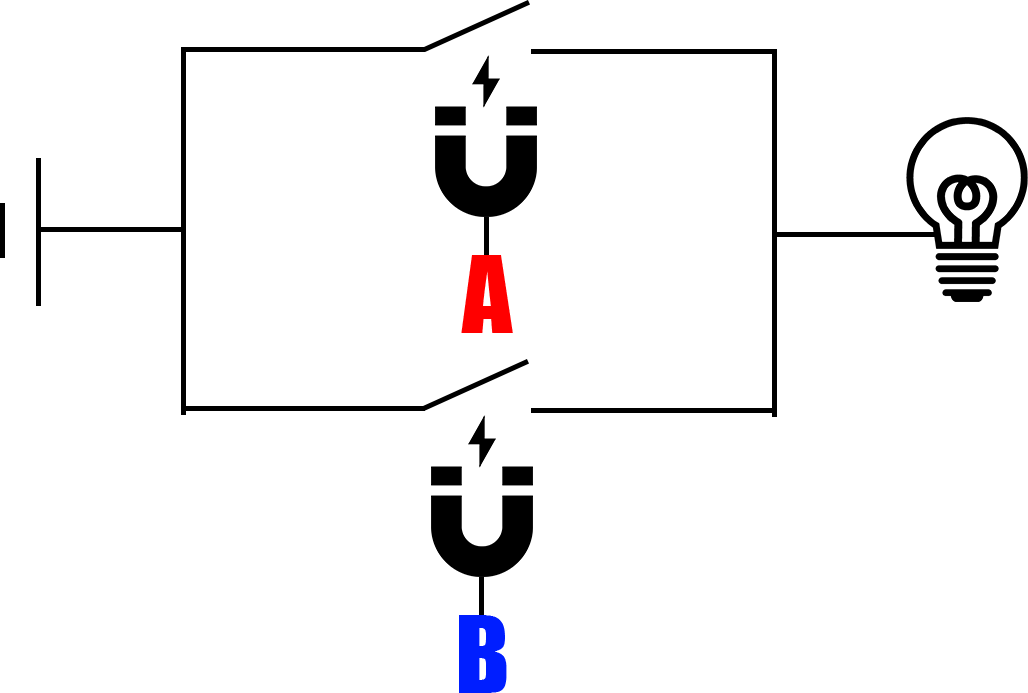
スイッチが両方ともOFFの時以外は豆電球が点灯するので、関係を表にすると以下です。

この関係は論理和回路(OR回路)と呼ばれるものです。
OR回路の図は簡略化して👇このように書き、
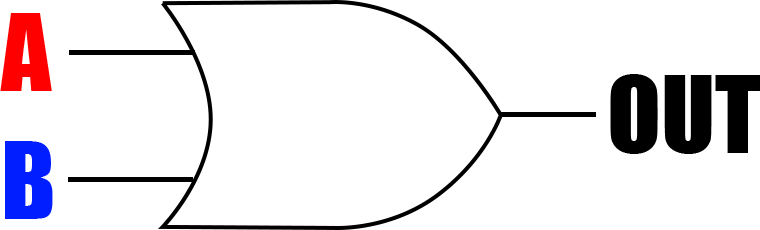
ベン図にしてみると斜線の部分を表します。
反対にするNOT回路
直列つなぎでAND回路、並列つなぎでOR回路と紹介してきましたが、あと一つ基本的な回路としてNOT回路というものがあります。
NOT回路はその名の通り入力を否定する(反対にする)回路で、先に真理値表を見せると

こういうことになります。シンプル。
回路を考えてみますと、例えばこんな感じでどうでしょう。

ちょっと分かりにくいかもしれませんが、もともと何もしていていない時はONになっているスイッチがあり、Aに電流を流すと磁力で引っ張られてスイッチが外れる、と考えて貰えば良いかなと思います。
もちろん現実のNOT回路はもっと違う形なんですが(というか先に紹介した2つの回路も)、原理を知るためのイメージはこの程度で問題ないかと思います。
NOT回路にも記号があり👇

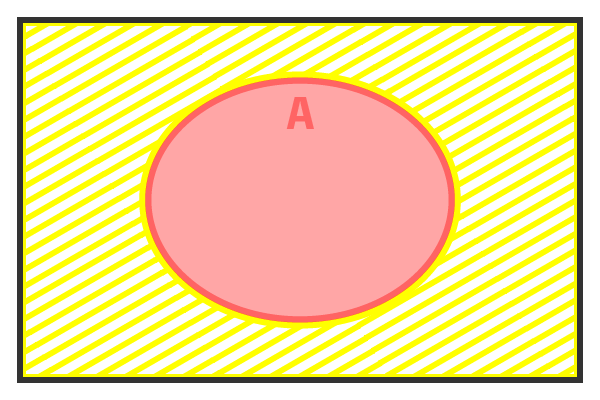
また、ベン図ではこうなります。
これらを組み合わせてXOR回路
AND回路、OR回路、NOT回路。
これらを組み合わせてXOR(排他的論理和)回路というものができます。
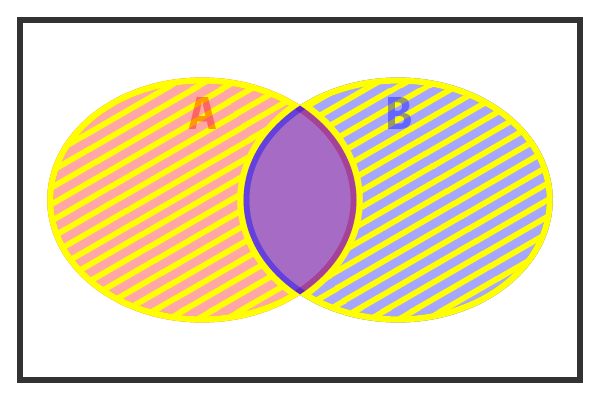
これは先にベン図を見せますと、
真理値をみてみると、

といったものです。
つまりは、AかB、どちらか一方がONの時のみ、出力されるということ。
この出力の結果をAND、OR、NOTを工夫して組み合わせることで実現します。
組み合わせ方は色々ありますが、一例を出しますと、
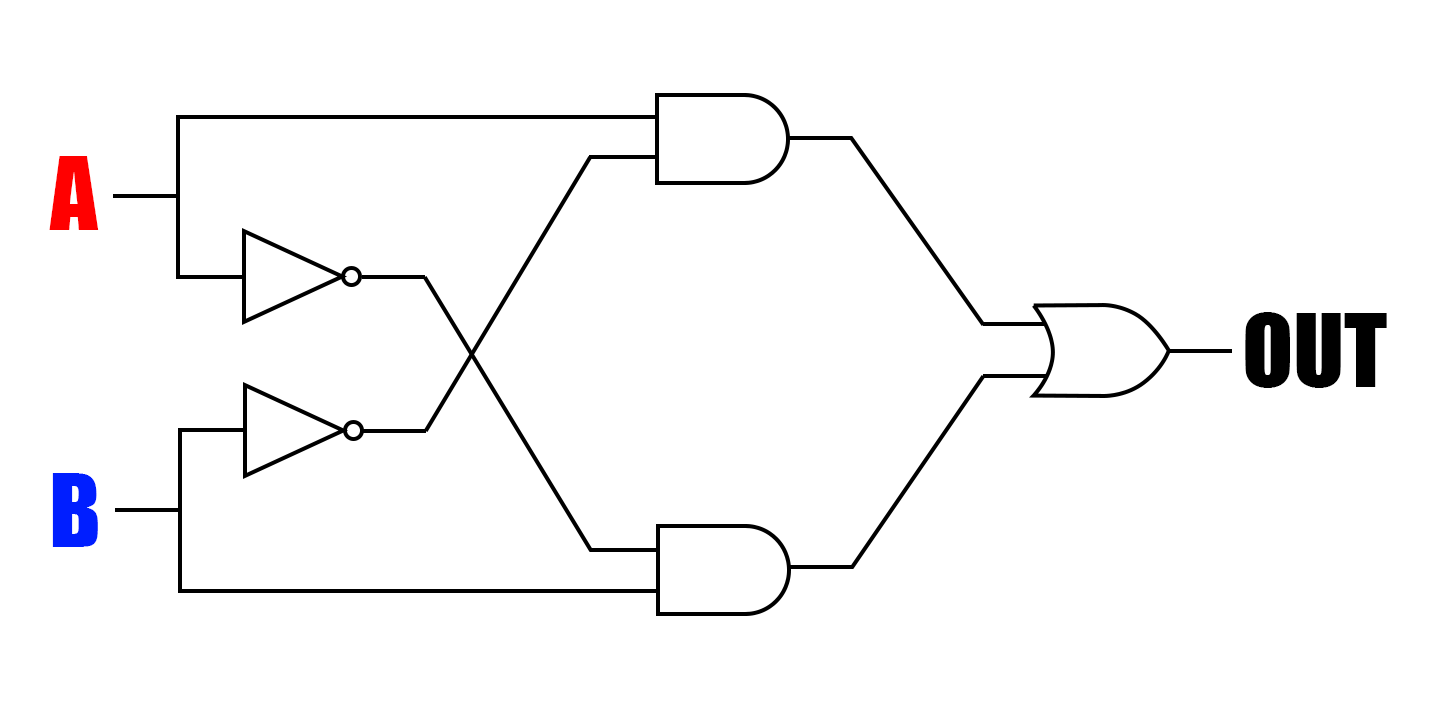
こんな風にNOT回路2個、AND回路2個、OR回路1個で望んだ出力を実現する回路ができます。
試しにAに0、Bに1を入力してみると、
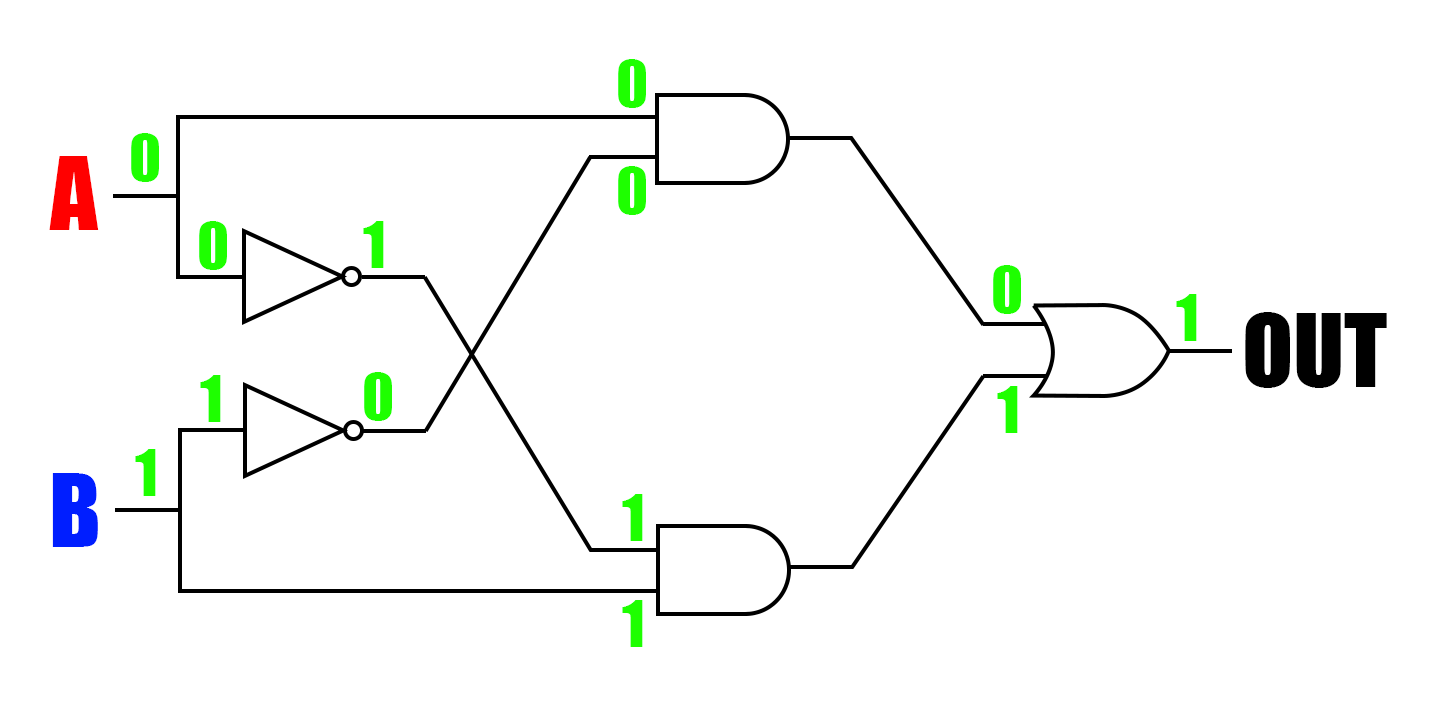
このように正しく1が出力されることが分かります。
うまいこと考えるものですよね。
他のパターンでも正しい結果が出るはずなので試しに適当な入力値を入れてみるとちょっとだけ理解が深まると思います。
そしてXOR回路の記号はこちらです👇
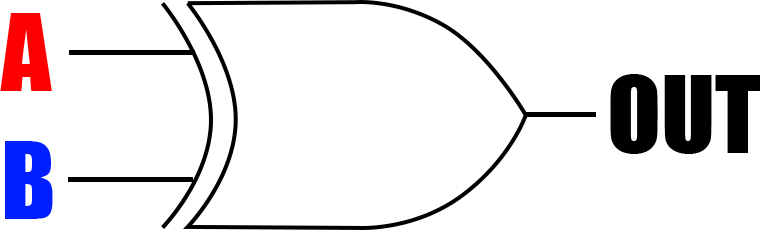
足し算ができれば四則演算はできる
さて、ここまで4つの回路の紹介をしてきましたが、ここで一度計算について整理します。
2進数での足し算
前編で書いたように機械は数字を2進数で表します。
その2進数での足し算ですが、やり方はやはり10進数と変わらず、同じ桁同士を足して数値の上限に来たら繰り上げるというものです。
3+5の計算を2進数でやってみるならば、3は2進数で「0011」、5は「0101」なので、
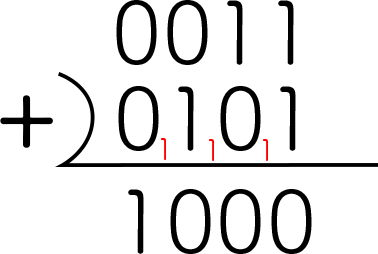
このように筆算で計算できます。(赤字は繰り上がり)
「1000」すなわち、10進数で8という答えになります。
足し算ができれば引き算はできる
続いて引き算ですが、引き算を「負の数の足し算」と考えることで可能です。
それでは2進数で負の数をどう表現するかというと、「足して0になる数」を作ることで負の数とします。
どういうことかというと、例えば-1の場合で考えてみましょう。
1に足すと結果が0になるような2進数、式で表すなら、
1 + (-1) = 0
1の2進数は「0001」なので、これに足すことで「0000」を作ることのできる数を-1とします。
一見無理そうに見えますが、4bit(4桁)で数字を表している場合、桁を溢れさせることで「0000」を作ることができます。
すなわち、4桁で数字を表すというルールの下では、あえて5桁の「10000」を作り出し、先頭の1を無視することで「0000」を作るということになります。
ということは-1を2進数(4bit)で表すと「1111」ということが分かります。(「0001」 に 「1111」 を 足すと繰り上げが続いて 「10000」になるため)
-1以外の数でも同様で、こんな感じ👇で表します。(4bitの場合)
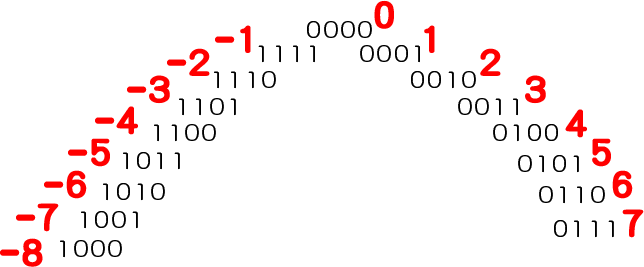
このように負の数を表すことで引き算も「負の数を足す」という形で可能になることが分かります。
足し算ができれば掛け算はできる
掛け算は足し算で表すことができるので掛け算も足し算ができれば可能です。
例えば、
2 × 3
は、「2を3回足す」と言い換えることができます。
2 + 2 + 2
ですので掛け算も原理的に可能ですね。
割り算は引き算ができればできる
割り算は「何回引くことができるか」という風に考えることで可能になります。
例えば、25 ÷ 6 = 4 ・・・ 1 という割り算は、
「25から6は何回引けるか」と考えることで答えが出ます。
25 – 6 = 19 (1回目)
19 – 6 = 13 (2回目)
13 – 6 = 7 (3回目)
7 – 6 = 1 (4回目)
5回目は引けないので、答えは「4余り1」。
このように割り算も「引き算が何回できるか」と考えることで原理的に可能になることが分かります。
電子回路を用いた2進数の足し算
これまでのことで、足し算さえできれば計算ができることが分かりました。
それではいよいよ、その足し算を電子回路を使って実現する仕組みを紹介します。
2進数での足し算のところで例に出した式を使いましょう。👇

この式をそれぞれの桁ごとに分解してみます。
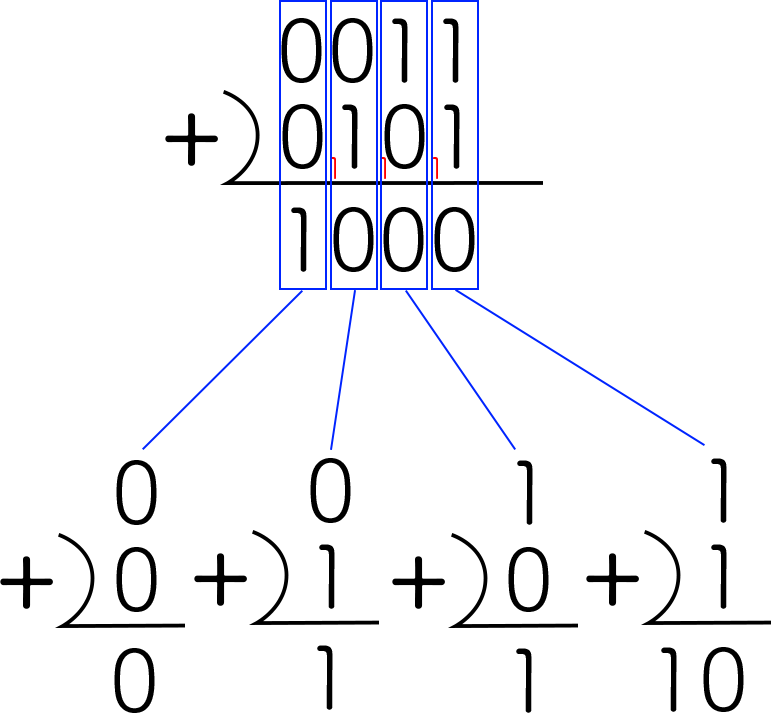
さらに分解した式にちょっと手を加えて、繰り上がりがない場合でも0の数字を入れて2桁に揃えます。
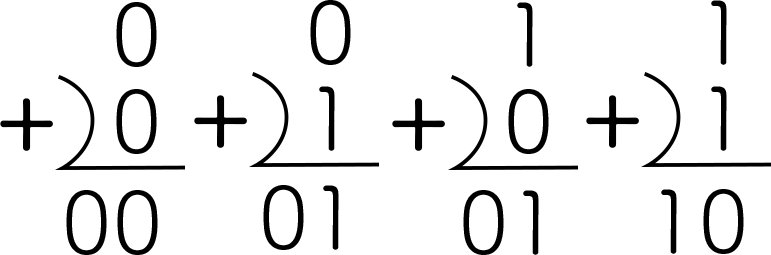
便宜上、分解した式の最初の数を「A」足す数を「B」答えの右の数を「S」繰り上がりに値する左の数を「C」と置きます。👇

こうして分解した4つの式に対して、「A、Bの値とSの関係」「A、Bの値とCの関係」を真理値表にしてみるとこのようになります。
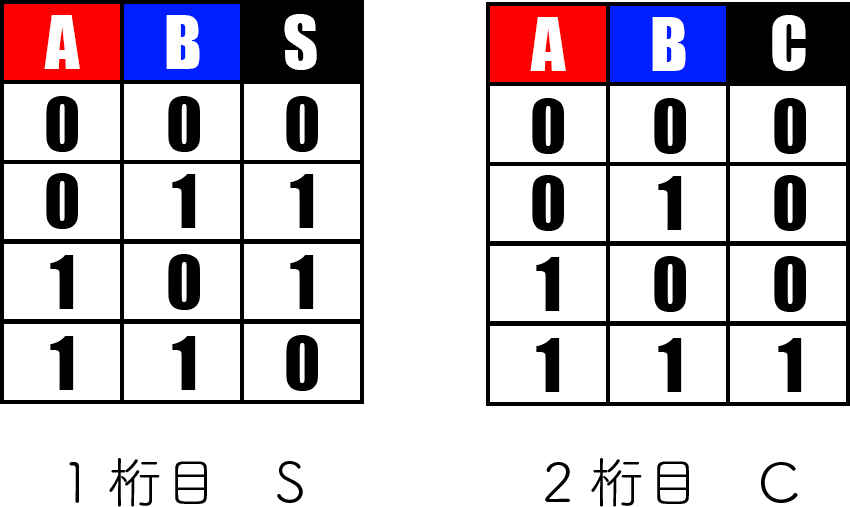
はて、この真理値表どこかで見たことがあります。
実は既に紹介した「XOR回路」と「AND回路」の真理値表と全く同じなのです。
よって、「S」と「C」はそれぞれ電子回路によって求められるということなのです!

と、いうことはA、Bの足し算の答えが知りたいとき、A、Bを「XOR回路」と「AND回路」に通すことで同じ結果を得られるということが判明しました。
これを「半加算器」と言います。
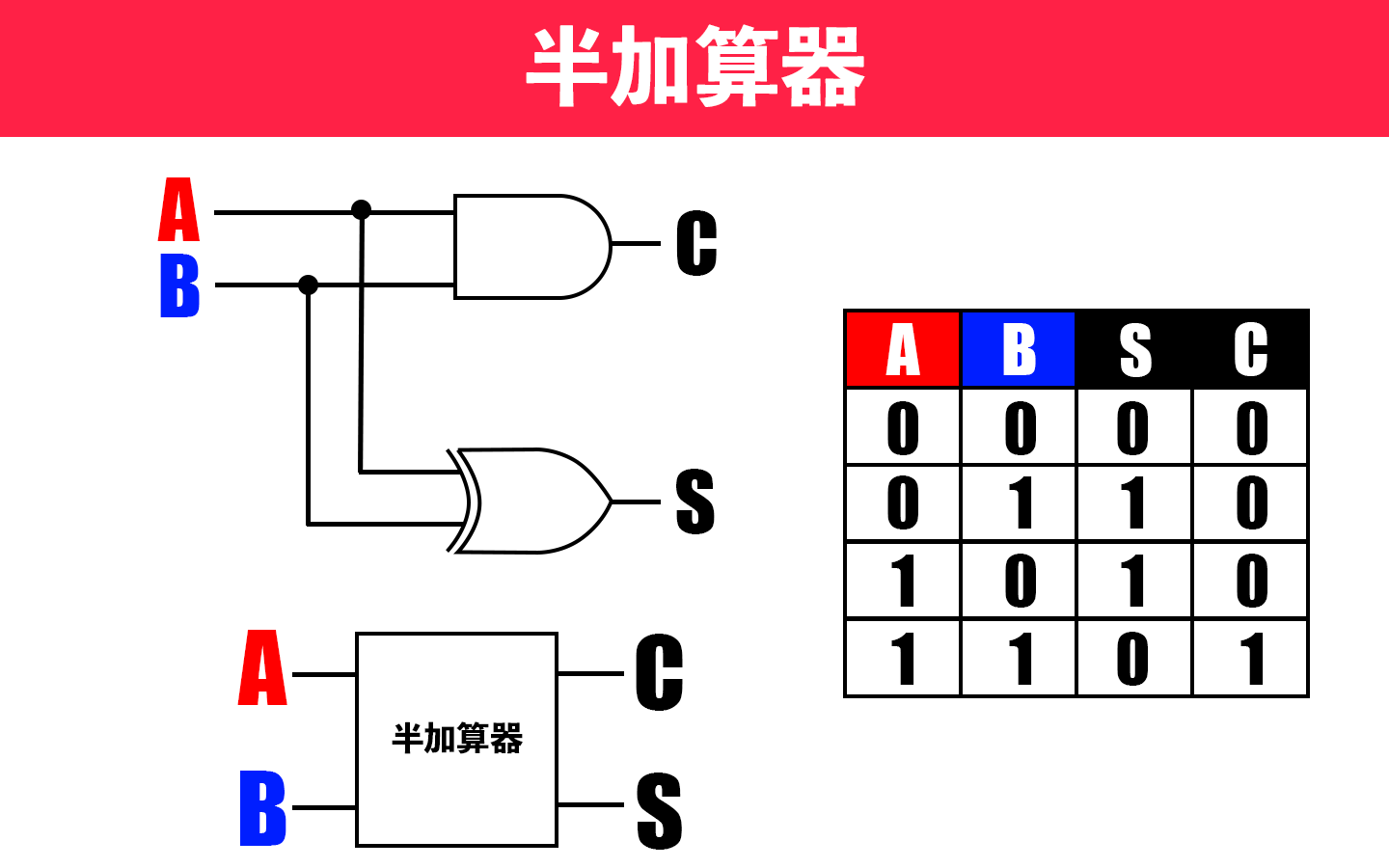
こうして、無事電子回路を用いて2進数の足し算ができるようになりました。
ただし、まだ不完全です。
半加算器では1桁の計算しかできません。
👇の式でいうと一番右の列の計算しかできないということです。

なぜなら、👆の式の右から2列目、3列目、4列目の計算では「前の桁からの繰り上がり」を考慮しなければならないからです。
それじゃあ考慮しようじゃないか。
ということで、入力値「A」「B」の他に「前の桁からの繰り上がりC’」を入れた計算を考えてみます。
ちょっとややこしくなりますので考えるのが面倒な方は読み飛ばしてください。
半加算器によってSが求められますが、このSに対して前の桁からの繰り上がりC’を足さなければなりません。(このSをS1と置いておきます)
S1とC’を足す。即ち、さらに半加算器に通すことになります。
その結果出てきた新たなS、CをS2、C2と置きましょう。
もう分かりにくいと思うので、ここまでを図表します。
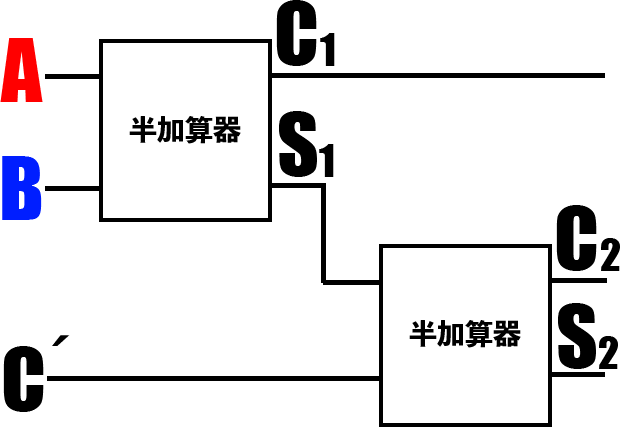
このS2ですが、他に足すものは何もないので確定となります。
あとは繰り上がりのCを考えれば良いことになりますが、👆の図でいうC1とC2に関して、「A」「B」の「0」「1」の組み合わせ4パターン全てを考えても「どちらも1になることはない」ということが分かります。
C1が1になるのは「A=1」「B=1」の時だけ ・・・①
C2が1になるのは「S1=1」「C’=1」の時だけど、S1が1になるのは「A、Bどちらか一方が1」の時だけ ・・・②
①と②が両立することはないのでC1とC2は「どちらか一方だけが1」もしくは「どちらも0」のパターンしかあり得ません。
よって最終的なCはC1、C2の繰り上がりなんてものは考慮せず、「C1、C2どっちかに1があるかどうか」だけを見ればいいことになり、
それは「どちらか一方でも1なら1を出力する」という「OR回路」の挙動と同じになります。
よって残りを作図してみると👇こうなります。
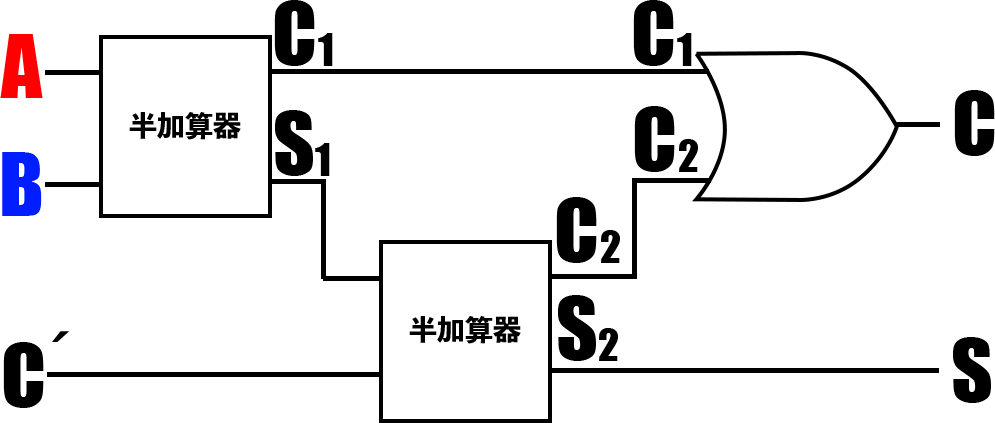
これで「前の桁からの繰り上がりも考慮した計算」ができる回路が完成しました。
これを「全加算器」と言います。
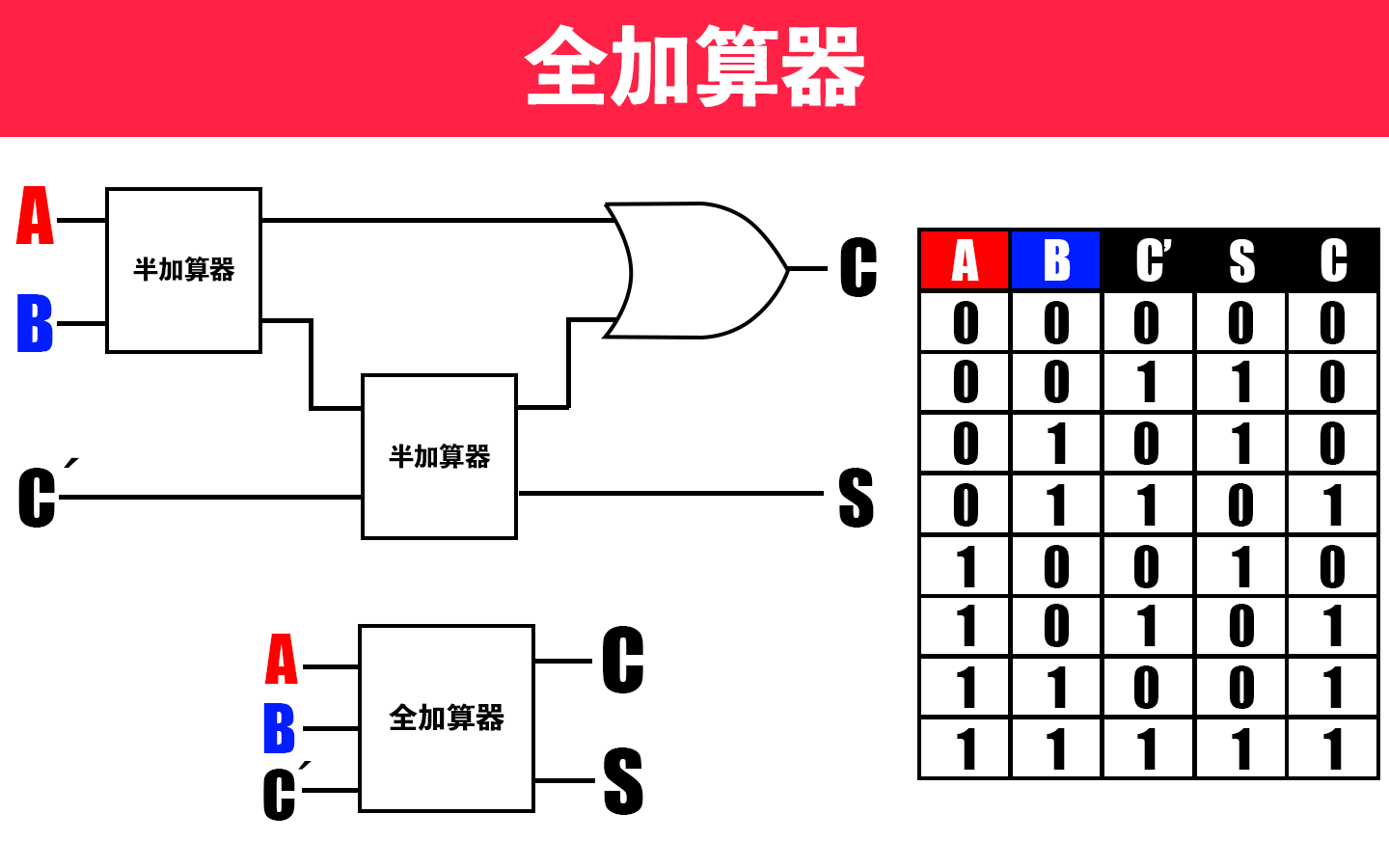
あとは、この半加算器と全加算器を組み合わせれば、何桁の足し算でも可能になります。👇

最初の桁は繰り上がりを考えなくていいので半加算器、その後の桁は前の桁からの繰り上がりを考えなければならないので全加算器ということですね。
終わりに
さて、これで足し算を電子回路を使って実現することができました。
前に書いたように原理的には足し算さえできれば他の四則演算も可能なので、
コンピューターはどうやって計算しているのか
の説明は終わりになります。
かなり語弊のある説明もあったかと思いますが、原理はこんな感じです。
電気を使って計算するなんでどういうことだろう? という状況からなんとなくでもイメージできるようになってもらえたなら幸いです。
いやぁ、昔の人はほんとにうまいこと考えるものですよね。
ここまで読んでいただきありがとうございました











